PROBABILIDAD Y ESTADÍSTICA DISTRIBUCIÓN DE PROBABILIDAD POISSON

Actualizado el 1 octubre 2020. La distribución de Poisson es una distribución de probabilidad discreta que modeliza la frecuencia de eventos determinados durante un intervalo de tiempo fijado a partir de la frecuencia media de aparición de dichos eventos. En otras palabras, la distribución de Poisson es una distribución de probabilidad.
Distribucion de Poisson

Distribución binomial — La distribución binomial es una distribución discreta de dos parámetros que cuenta el número de éxitos en N pruebas independientes con la probabilidad de éxito p.La distribución de Poisson es el caso limitante de una distribución binomial donde N se acerca a infinito y p a cero mientras Np = λ.Consulte Comparar las pdf de la distribución binomial y de Poisson.
Fórmula de distribución de Poisson y su significado en finanzas invatatiafaceri.ro

Las distribuciones de Poisson se utilizan para encontrar la probabilidad de que ocurra un evento en un intervalo de tiempo, área, volumen o distancia. Las distribuciones de Poisson se pueden aplicar a muchos campos de estudio, incluidos la ciencia y los negocios. Por ejemplo, un gerente comercial puede usar una distribución de Poisson para.
DISTRIBUCIÓN DE POISSON EN EXCEL EJERCICIO RESUELTO YouTube

Ejemplos y fórmula del proceso de Poisson. Ejemplo 1. Estos son ejemplos de eventos que pueden describirse como procesos de Poisson: Mi computadora falla en promedio una vez cada 4 meses. Las urgencias hospitalarias reciben una media de 5 casos muy graves cada 24 horas. El número de coches que pasan por un punto, en una carretera pequeña, es.
Poisson Distribution Formula and Meaning in Finance
:max_bytes(150000):strip_icc()/poisson-56a8fa9e3df78cf772a26eb0.jpg)
La distribución de Poisson fue propuesta por primera vez por Simeón Poisson en libro publicado en 1837. A medida que pasaron los años, el número de aplicaciones comenzó a aumentar, sobre todo el siglo XX y con la aparición de las computadoras en el siglo XXI permitió incrementarlas aún más. La distribución de Poisson es una.
Distribución de Probabilidad Poisson Capítulo 6 YouTube

Fórmula y ecuaciones. La forma matemática de la distribución de Poisson es la siguiente: - μ (también a veces denotado como λ) es la media o parámetro de la distribución. - Número de Euler: e = 2.71828. - La probabilidad de obtener y = k es P. - k es el número de éxitos 0, 1,2,3…. - n es el número de pruebas o eventos.
Poisson Distribution

Tenga en cuenta que la distribución de Nt depende de los parámetros r y t sólo a través del producto rt. La distribución se denomina distribución de Poisson con parámetro rt. En el experimento de Poisson, variar r y t con las barras de desplazamiento y anotar la forma de la función de densidad de probabilidad.
Poisson Distribution / Poisson Curve Simple Definition Statistics How To
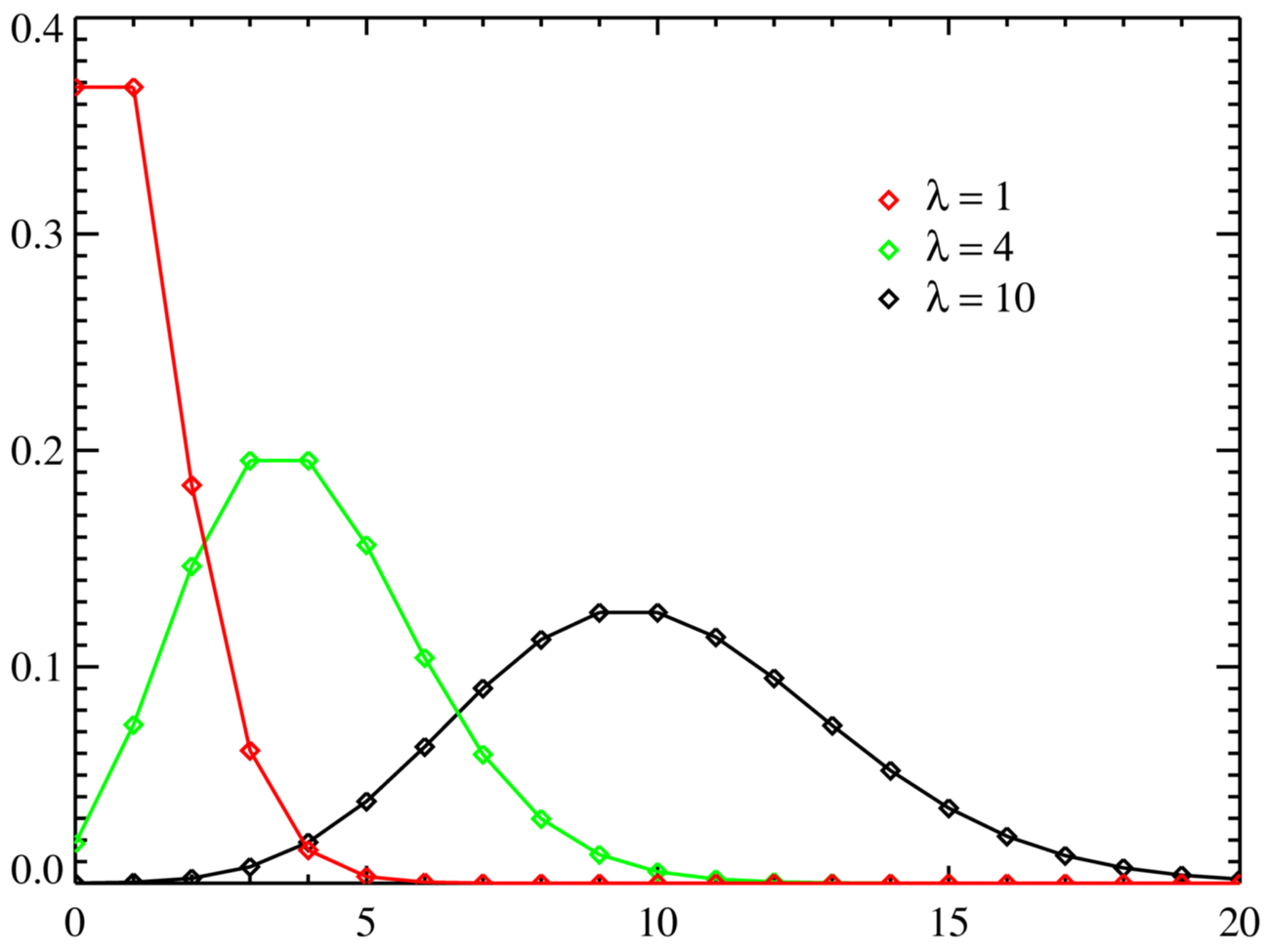
Otra distribución de probabilidad útil es la distribución de Poisson o distribución del tiempo de espera. Esta distribución se utiliza para determinar cuántos empleados de caja son necesarios para mantener el tiempo de espera en la fila a niveles especificados, cuántas líneas telefónicas son necesarias para evitar que el sistema se sobrecargue, y muchas otras aplicaciones prácticas.
Distribución de Poisson Ejemplos resueltos YouTube

Usando la distribución de Poisson: Calcular μ = np = 200(0.0102) ≈ 2.04. P(x = 10) = poissonpdf(2.04, 10) ≈ 0.000045. Esperamos que la aproximación sea buena porque n es grande (mayor que 20) y p es pequeña (menos de 0.05). Los resultados son cercanos, ambas probabilidades reportadas son casi 0. Ejercicio 4.7.7.
Distribución de Poisson Wikipedia, la enciclopedia libre
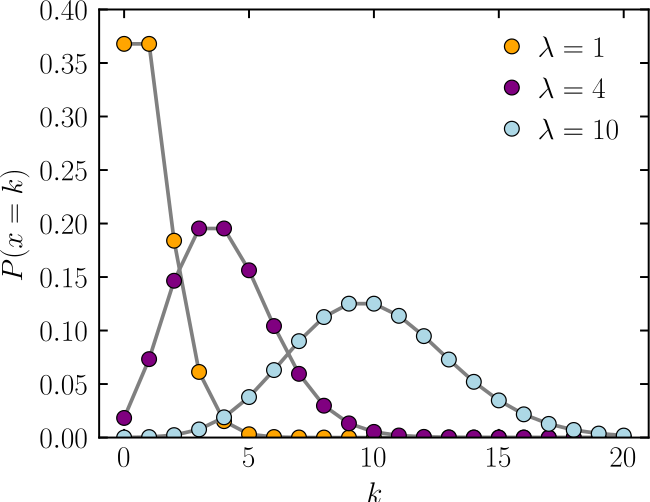
Hay dos características principales de un experimento de Poisson. La distribución de probabilidad de Poisson da la probabilidad de que se produzca un número de eventos en un intervalo fijo de tiempo o espacio si estos eventos se producen con una tasa promedio conocida y con independencia del tiempo transcurrido desde el último evento. Por ejemplo, un editor de libros podría estar.
Distribución de Poisson Teoría y ejercicio resuelto YouTube
Fórmula y ecuaciones. La forma matemática de la distribución de Poisson es la siguiente: - La variable aleatoria es y. - μ (también a veces denotado como λ) es la media o parámetro de la distribución. - Número de Euler: e = 2.71828. - La probabilidad de obtener y = k es P. - k es el número de éxitos 0, 1,2,3….
Distribución de Poisson Ejemplo 1 YouTube

A Poisson distribution is a discrete probability distribution. It gives the probability of an event happening a certain number of times ( k) within a given interval of time or space. The Poisson distribution has only one parameter, λ (lambda), which is the mean number of events. The graph below shows examples of Poisson distributions with.
DISTRIBUCION DE POISSON(2022) Ejemplos Ejercicios de Matemáticas

The Poisson distribution is a good approximation of the binomial distribution if n is at least 20 and p is smaller than or equal to 0.05, and an excellent approximation if n ≥ 100 and n p ≤ 10. [31] Letting and be the respective cumulative density functions of the binomial and Poisson distributions, one has:
Capítulo 06, Distribuciones discretas de probabilidad

La distribución de Poisson tiene un parámetro característico, que se representa con la letra griega λ e indica el número de veces que se espera que ocurra el evento estudiado durante un intervalo dado. En general, la distribución de Poisson se usa para modelizar estadísticamente sucesos cuya probabilidad de ocurrencia es muy baja.
Ejemplo Distribución de Poisson YouTube

Calcular probabilidades de la distribución de Poisson paso a paso. La calculadora encontrará las probabilidades simples y acumulativas, así como la media, la varianza y la desviación estándar de la distribución de Poisson. Tasa media de éxito \lambda λ: Valor de una variable aleatoria X X: Si la calculadora no calculó algo o ha.
Distribución de Poisson utilizando Excel Ejercicio 2 Probabilidades Acumuladas YouTube
The Poisson distribution is often used in quality control, reliability/survival studies, and insurance. Data are counts of events (nonnegative integers with no upper bound). All events are independent. Average rate does not change over the period of interest. The following graphs represent Poisson distributions with different lambdas.
.