FUNCIONES. Identificar cuáles relaciones son funciones. Ejecicios 1 al 6 YouTube

Aplicas funciones especiales y transformaciones de gráFcas. 51. Figura 2.4. Función escalonada.. Todas las funciones polinomiales son continuas. Funciones discontinuas.. que hacen cero el denomina-dor. Funciones escalonadas. Existen funciones que se deFnen a través de intervalos . cuyo dominio es (−∞,∞), sin embargo, no son.
4. Representación gráfica de funciones

Una Función Especial es aquella que pertenece al siguiente conjunto de funciones elementales, tales como: función constante, identidad, cuadrática, y muchos.
Tipos de Funciones Algebraicas y sus Gráficas Neurochispas
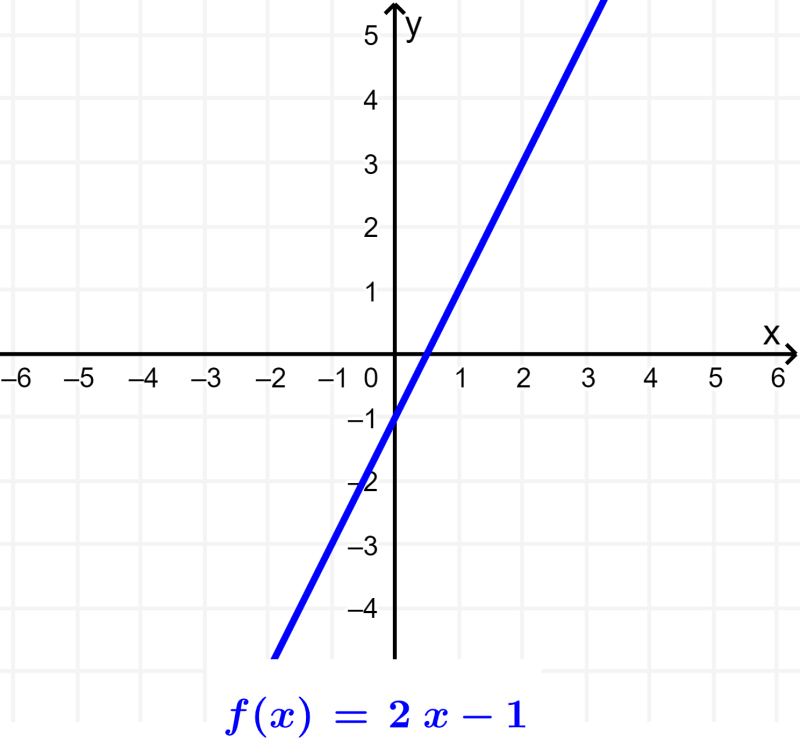
Ejercicio 6.6.5. En el espacio tridimensional, tenemos funciones de proyección que van sobre los tres ejes de coordenadas ( π1, π2 y π3) y también tenemos proyecciones sobre planos de coordenadas. Por ejemplo, π12: R × R × R R × R, definido por. π12((x, y, z)) = (x, y) es la proyección en el plano de y coordenadas x —.
Clasificación de las funciones reales YouTube

Las funciones especiales son aquellas que no pueden expresarse como una combinación finita de funciones elementales, mediante operaciones de suma, resta, producto, división o composición de funciones. Estas funciones surgen en muchos problemas de aplicación en la Física y otras ciencias, por lo que son muy importantes.
Qué es una función y una relación en matemáticas Concepto de función YouTube

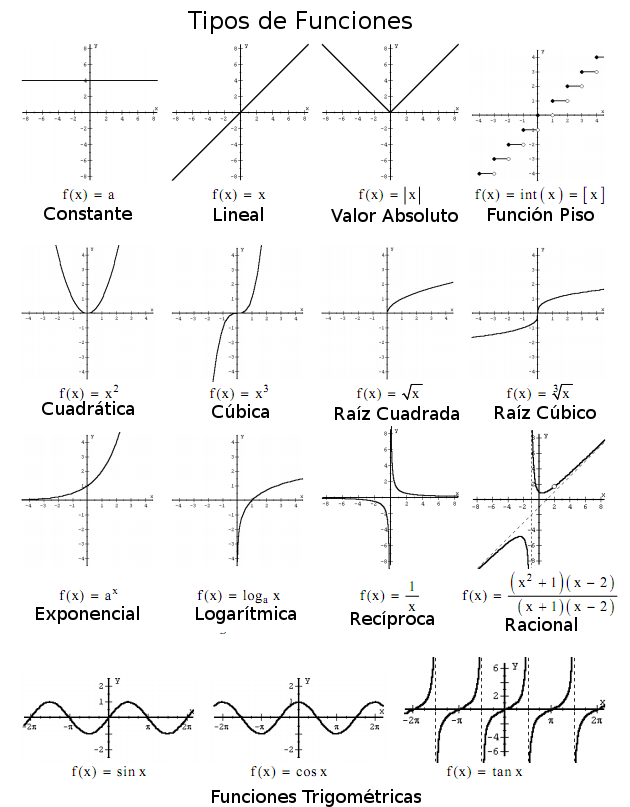
Una Función Especial es aquella que pertenece al siguiente conjunto de funciones elementales: Función constante: f (x) = m (donde m es una constante) Función identidad: f (x) = x. Función cuadrática: f (x) = x2. Función cúbica: f (x) = x3. Función raíz: f (x) = √x (siempre que x sea mayor o igual a 0)
Gráfica de una función exponencial usando técnicas de graficación YouTube

Comenzamos con una colección de funciones especiales, llamadas polinomios ortogonales clásicos. Estas incluyen funciones polinómicas tales como los polinomios Legendre, los polinomios Hermite, los polinomios Tchebychef y Gegenbauer. Además, las funciones de Bessel ocurren con bastante frecuencia. Pasaremos más tiempo explorando las.
Tipos de Funciones Algebraicas y sus Gráficas Neurochispas
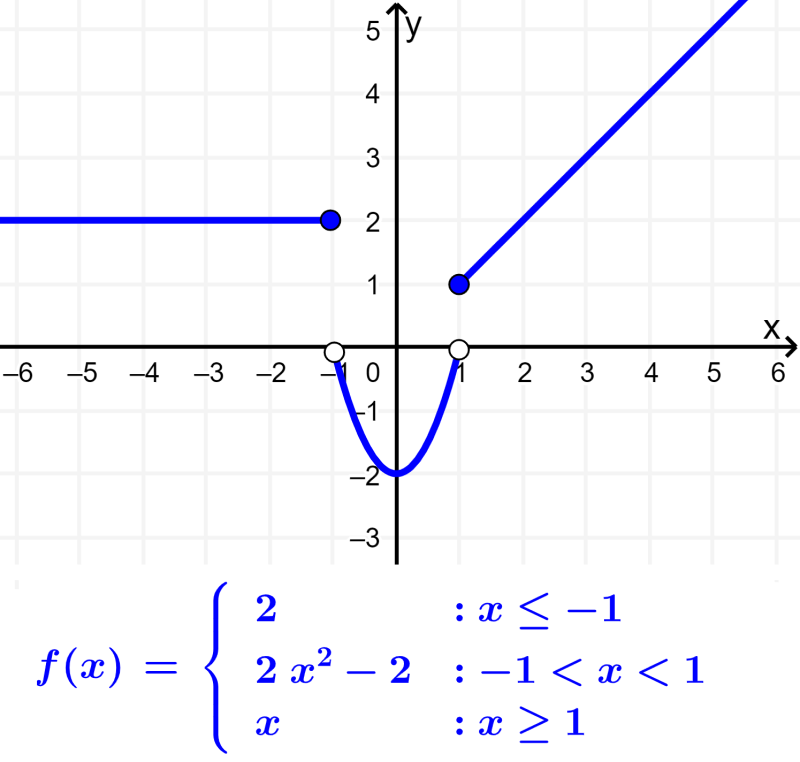
20 unidades · 405 habilidades. Unidad 1 Introducción al álgebra. Unidad 2 Resolución de ecuaciones básicas y desigualdades (una variable, lineal) Unidad 3 Ecuaciones lineales, funciones y gráficas. Unidad 4 Sucesiones. Unidad 5 Sistemas de ecuaciones. Unidad 6 Desigualdades con dos variables. Unidad 7 Funciones.
“FUNCIONES MATEMÁTICAS CONCEPTOS BÁSICOS” Mind Map
.gif)
Una función especial es una función matemática particular, que por su importancia en el campo del análisis matemático, análisis funcional, la física y otras aplicaciones, posee nombres y designaciones más o menos establecidos. No existe una definición general de las mismas, pero la lista de funciones matemáticas contiene funciones que.
Catalogo de Funciones PDF Relaciones matematicas Funciones especiales

Las funciones especiales se definen como soluciones analíticas específicas para ecuaciones diferenciales que se utilizan para modelar fenómenos complejos en matemáticas, física e ingeniería. Según la real academia española, no existe una definición específica para funciones especiales como término único. 📋 Copiar.
Derivadas de funciones especiales YouTube

Una función especial es una función (que suele llevar el nombre de uno de los primeros investigadores de sus propiedades) que tiene un uso particular en la física matemática o en alguna otra rama de las matemáticas. Algunos ejemplos destacados son la función gamma, la función hipergeométrica, la función Whittaker y la función G de Meijer.
Cuadro Comparativo de Funciones PDF Función (Matemáticas) Logaritmo

Las funciones especiales son funciones matemáticas particulares que tienen nombres y notaciones más o menos establecidas debido a su importancia en el análisis matemático , análisis funcional , geometría , física u otras aplicaciones. El término se define por consenso y, por lo tanto, carece de una definición formal general, pero la.
Matematica II 2014 Semestre A Tipos de Funciones
Determina si las siguientes funciones son inversas entre sí: Si las dos funciones son inversas entre sí, se cumplirán las siguientes 2 condiciones: Por lo tanto, vamos a comprobar si se cumplen ambas ecuaciones. Primero comprobamos . De modo que sí se cumple. Ahora vamos a comprobar la igualdad . Y la condición de invertibilidad también.
funciones Mind Map
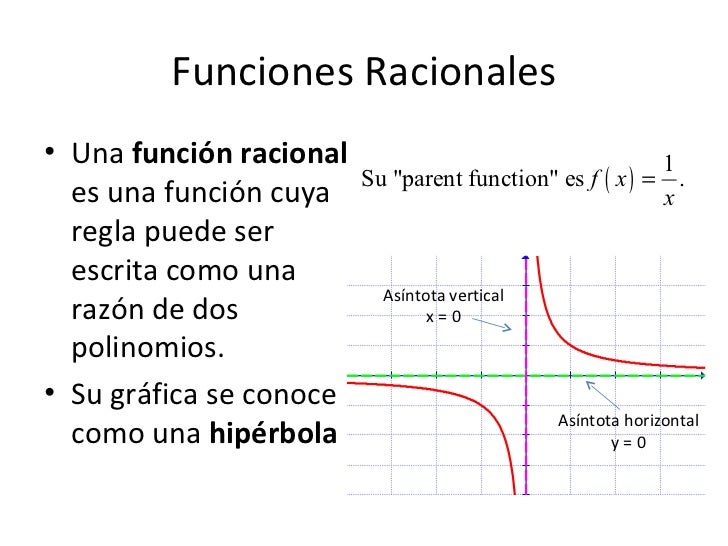
Concepto de funciones especiales Las funciones especiales se clasifican en: Funciones explícitas. La variable dependiente está despejada. Ejemplo: y = f (x).Funciones implícitas. La función está dada por una ecuación; es decir, la variable dependiente no está despejada. Ejemplo: x2y − 4y = 2 Funciones continuas. Su gráfico no presenta ningún punto aislado, saltos o…
¿Qué son las funciones y para qué sirven?
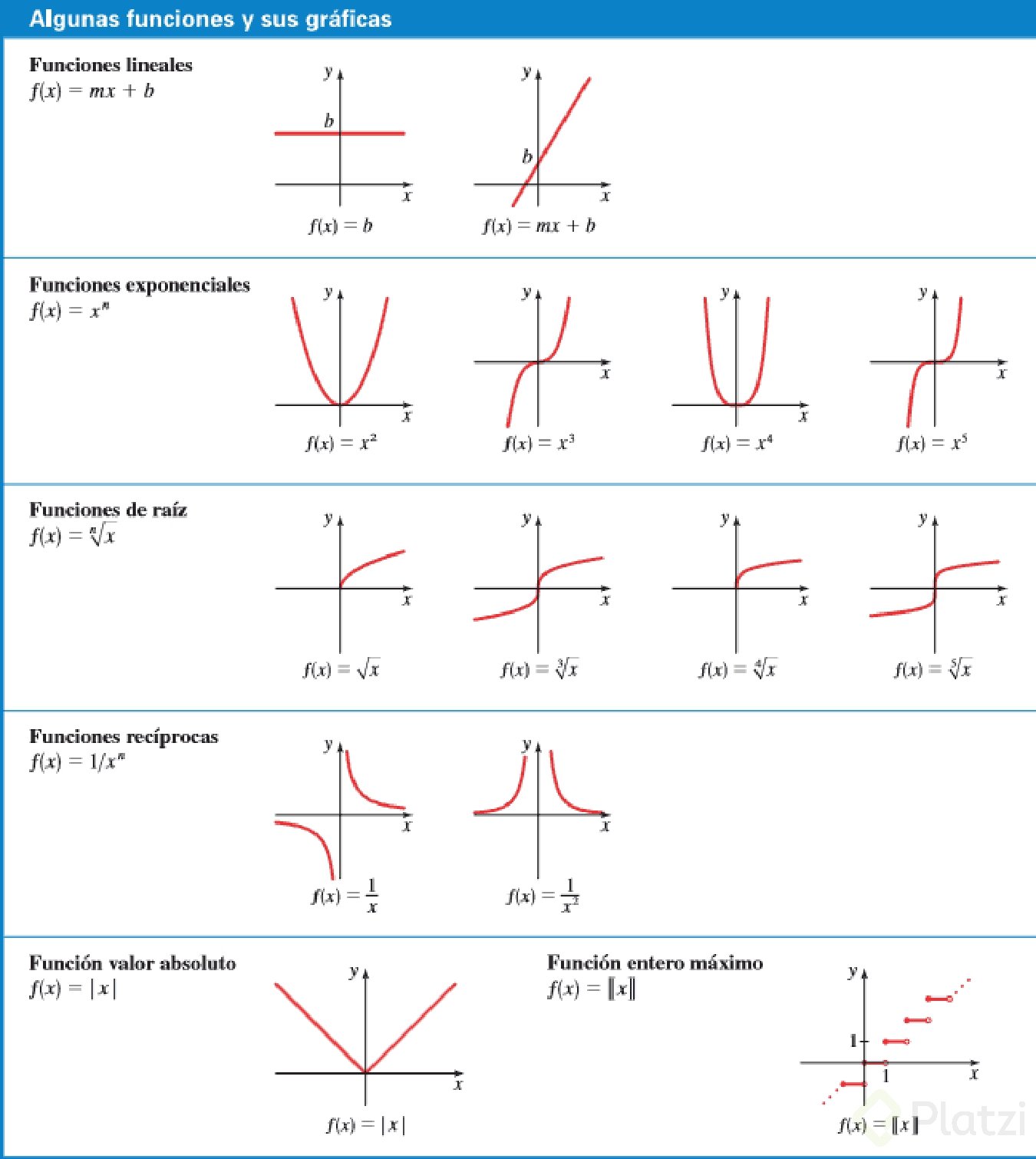
Las funciones hiperbólicas son combinaciones especiales de exponenciales e x y e-x y se denominan como seno, coseno….hiperbólico. Al igual que con las funciones trigonométricas, también llamadas "circulares", hay 6 funciones hiperbólicas: -Seno hiperbólico senh x: La función seno hiperbólico. Fuente: F. Zapata a través de Geogebra.
Funciones Función exponencial. 4º de ESO matemáticas YouTube
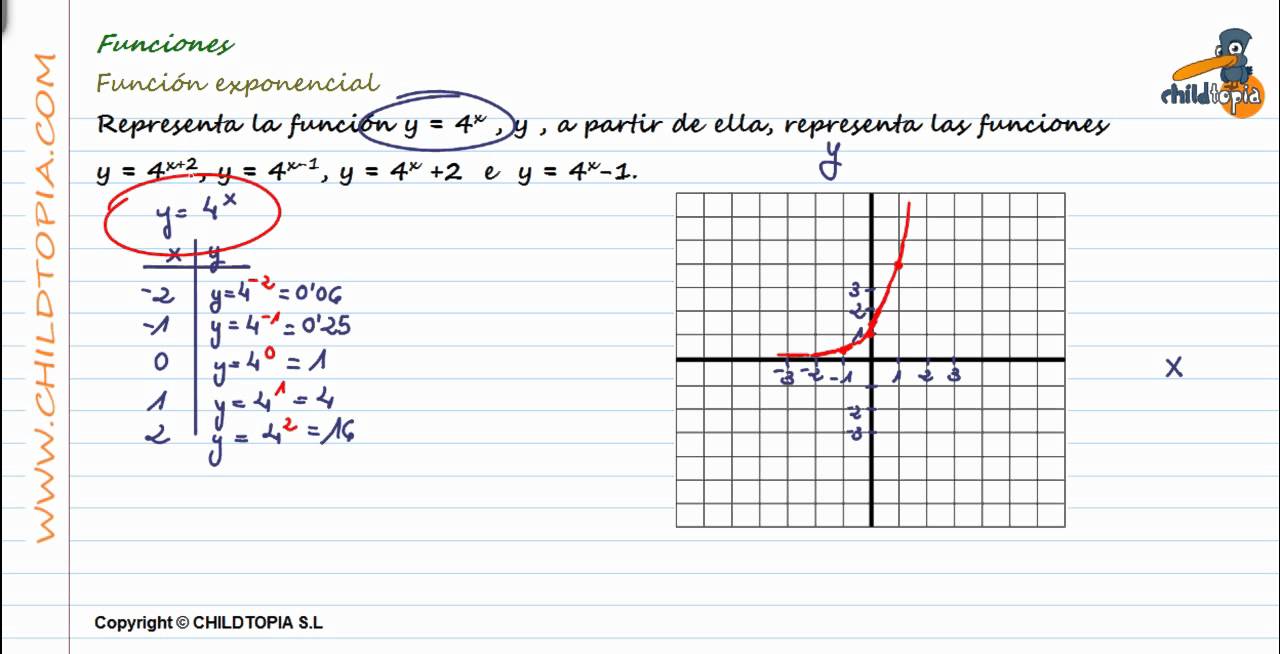
Función tangente: Función cosecante: Función secante: Función cotangente: Tal y como hemos indicado, estas son las funciones matemáticas más básicas que se pueden encontrar y es que existen algunas más complejas que no son cometido de este artículo. Además, estas funciones solo son la base, ya que, a partir de la composición de.
Tipos de Funciones Algebraicas y sus Gráficas Neurochispas
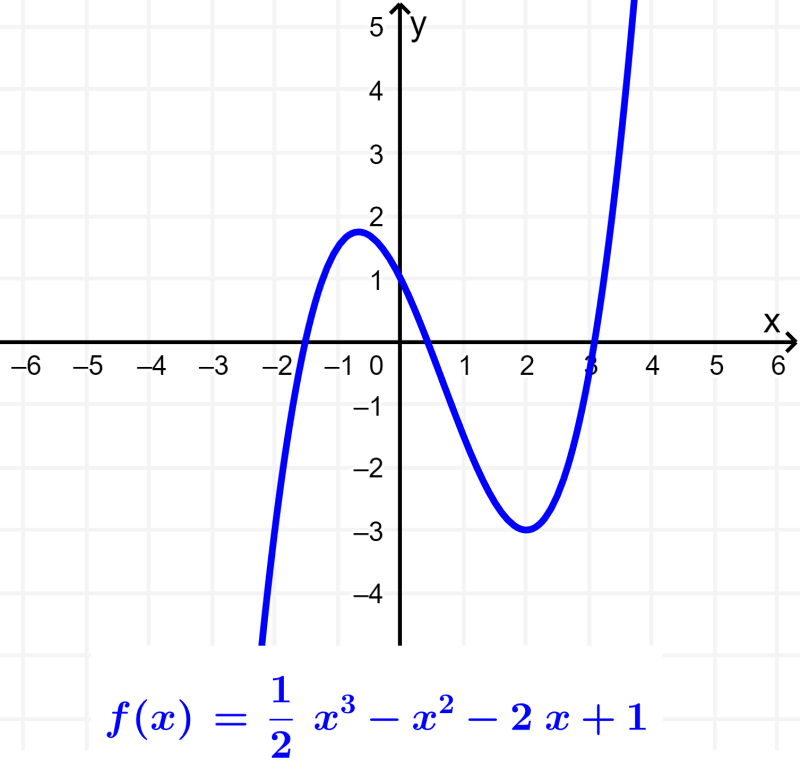
Función especial. Una función especial es una función matemática particular, que por su importancia en el campo del análisis matemático, análisis funcional, la física y otras aplicaciones, posee nombres y designaciones más o menos establecidos. No existe una definición general de las mismas, pero la lista de funciones matemáticas.
.